The Random Programs¶
The PyRat workspace comes with four players that make random moves: Random1, Random2, Random3, and Random4.
In this tutorial, we will go through the code of these players to understand how they work.
In a next tutorial, we will see how to write a new player, based on what we learned here.
Getting Started¶
Open your VSCode workspace and navigate to the players directory.
In addition to the TemplatePlayer class, that we already mentioned in the overview, you will find the following files:
We also provide in the games directory a script that visualizes the behavior of these players in a game.
We will not go through this script in details, but you can find it here:
Let’s go through the code of these players to understand how they work.
The Random1 Player¶
Documentation¶
The program starts with a global documentation that explains what it contains.
It is always good to add a small text like this, for you (or the other users of you code) to remember what you do.
Also, this particular type of comments (""" ... """) is parsed when producing the documentation files, as you did during installation.
You will find multiple places in Random1.py with documentation.
In the following blocks of code, we will drop them for readability.
# This file is part of the PyRat library.
# It describes a player that can be used in a PyRat game.
# It is meant to be used as a library, and not to be executed directly.
# Please import this file from a game script using the following syntax:
# from players.Random1 import Random1
"""
This module provides a player that performs random actions in a PyRat game.
It is a simple player that does not take into account the maze structure.
"""
Imports¶
The next thing you will find in this file is a series of imports.
In particular, we import the random module, which is part of the Python standard library.
It provides functions to generate random numbers, which we will use to make the player move randomly.
Finally, we import the classes that we need from the PyRat library.
# External imports
import random
# PyRat imports
from pyrat import Player, Maze, GameState, Action
Definition of the Class¶
A PyRat player should start with the following lines.
When writing your own programs, you will have to change the class name (here, Random1) for a name of your choice.
Often, the class name will be the same as the file name, without the .py extension, starting with a capital letter, and without any spaces or special characters.
Also, note that all PyRat players should inherit from class Player (defined in the pyrat module).
This is done by adding (Player) after the class name below.
By doing so, all players you will write will have access to the attributes (data) and methods (functions) defined in the Player class.
In particular, you can access the get_name(...) method, that will be useful to know where you are in the maze, as shown later on this page.
class Random1 (Player):
The Constructor __init__(...)¶
There is a particular method called __init__(...) that is called when you instantiate a class, i.e., when you run the code p = Random1(...).
This method should always start with the argument self, and finish with arguments *args, **kwargs (a good convention).
You can add all the arguments you want in the middle.
Also, this method’s body should always start with super().__init__(*args, **kwargs).
This line allows to pass the extra arguments in args and kwargs to the parent constructor.
In our case, these arguments are name and team, defined in the constructor of class Player.
Here, besides these default operations, we do not do anything special in the constructor. We are going to change that later in the other players.
def __init__ ( self,
*args: object,
**kwargs: object
) -> None:
# Inherit from parent class
super().__init__(*args, **kwargs)
The preprocessing(...) and postprocessing(...) methods¶
As Random1 does nothing during the preprocessing and postprocessing phases, we do not need to implement the preprocessing(...) and postprocessing(...) methods.
We will introduce the former later in this tutorial, and the latter in a more advanced tutorial.
The turn(...) Method¶
The main part of the player is the turn(...) method.
This method is called at each turn of the game, and it should return an action that the player wants to perform.
In our case, we want the player to move randomly.
For code readability, we are going to define a helper function called find_next_action(...).
This function will choose a random action from the list of possible actions defined in the Action enum.
def find_next_action (self) -> Action:
# Choose a random action to perform
action = random.choice(list(Action))
return action
Using this function, we can now implement the turn(...) method.
@override
def turn ( self,
maze: Maze,
game_state: GameState,
) -> Action:
# Return an action
action = self.find_next_action()
return action
The @override decorator is used to indicate that this method overrides a method from the parent class.
This is not mandatory, but it is a good practice to use it, as it helps to detect errors in the code.
A Game with Random1¶
If you want to run the player Random1, you can use the script visualize_random_players provided in the games directory.
Or, you can create your own game script.
Let’s do that for the sake of this tutorial.
First, create a new file in the
gamesdirectory calledmy_random1_game.py.Then, add the following minimal code to this file:
# PyRat imports from pyrat import Game from players.Random1 import Random1 # Instantiate a game with a few arguments game = Game(maze_width=15, maze_height=13, nb_cheese=1) # Instantiate the player # If we do not specify a name, the player will be named "Random1" player = Random1() game.add_player(player) # Start the game stats = game.start()
Finally, run the script from your VSCode workspace. You should see a window opening with the player moving randomly in the maze.
The Random2 Player¶
The second random player is a bit more intelligent.
Moving like Random1 has the drawback of sometimes running into walls, or maybe returning an action that does nothing (Action.NOTHING).
Here, we are going to return an action at random, among those that lead somewhere.
To obtain this information, we will use the arguments provided by the PyRat game to the turn(...) method.
Definition of the Class¶
Let’s start from file Random1.py to build file Random2.py.
First, we change the class name to Random2:
class Random2 (Player):
The turn(...) Method¶
Now, let’s update the find_next_action(...) method to return a random valid action.
To do so, we will need to use the maze map and current game configuration, received by turn(...) as arguments maze (an object of class Maze, defined in the pyrat module) and game_state (an object of class GameState, defined in the pyrat module).
In particular, game_state contains the current location of the player in the maze, that you can retrieve using its attribute game_state.player_locations.
This is a dictionary that maps player names to their current location in the maze.
You can retrieve your own location using the method get_name(...) defined in the parent class Player.
Combining these methods, you can retrieve your current location in the maze with the following code: my_location = game_state.player_locations[self.get_name()].
Now, we need to determine which actions are valid.
The Maze class has a method called get_neighbors(...) that returns the neighbors of a given location.
We are going to use this method to retrieve the accessible neighbors of our current location.
Finally, we just select one of these neighbors at random, and return the corresponding action.
Here is the complete code of the find_next_action(...) method.
Note that for this method to be able to use the maze and game_state arguments, we need to add them to the method signature.
def find_next_action ( self,
maze: Maze,
game_state: GameState,
) -> Action:
# Choose a random neighbor
my_location = game_state.player_locations[self.get_name()]
neighbors = maze.get_neighbors(my_location)
neighbor = random.choice(neighbors)
# Retrieve the corresponding action
action = maze.locations_to_action(my_location, neighbor)
return action
In coherence with these changes, we also need to update the turn(...) method to pass the maze and game_state arguments to the find_next_action(...) method.
@override
def turn ( self,
maze: Maze,
game_state: GameState,
) -> Action:
# Return an action
action = self.find_next_action(maze, game_state)
return action
A Game with Random2¶
If you want to run the player Random2, you can adapt the script you created for Random1.
You just need to import Random2 instead of Random1, and to instantiate a Random2 player instead of a Random1 player.
Here is the complete code of the game script:
# PyRat imports
from pyrat import Game
from players.Random2 import Random2
# Instantiate a game with a few arguments
game = Game(maze_width=15, maze_height=13, nb_cheese=1)
# Instantiate the player
# If we do not specify a name, the player will be named "Random2"
player = Random2()
game.add_player(player)
# Start the game
stats = game.start()
Running this script will open a window with the player moving randomly in the maze, but without hitting walls or returning actions that do nothing.
The Random3 Player¶
In the third random player, we are going to add a bit more intelligence. This player will try to move to an unvisited cell, if possible. If no unvisited cell is available, it will move randomly among the valid actions.
Contrary to the previous players, we now need to store information across turns.
To do so, we are going to add an attribute to the class, called visited_cells.
At each turn, we will add the current cell to this set of visited cells.
Definition of the Class¶
Let’s start from file Random2.py to build file Random3.py.
First, we change the class name to Random3:
class Random3 (Player):
The Constructor __init__(...)¶
Now, we need to add the visited_cells attribute to the class.
To do so, we add a new line in the constructor, after the call to the parent constructor.
This attribute will be a set that will store the visited cells.
A set is a data structure that allows to store unique elements, and to check if an element is in the set in constant time.
Contrary to a list, a set does not allow to store duplicate elements, and is not ordered.
Adding an already existing element to a set does nothing, and checking if an element is in the set is done in constant time.
Here is the complete code of the constructor:
def __init__ ( self,
*args: object,
**kwargs: object
) -> None:
# Inherit from parent class
super().__init__(*args, **kwargs)
# We create an attribute to keep track of visited cells
# We will initialize it in the ``preprocessing()`` method to allow the game to be reset
# Otherwise, the set would keep the cells visited in previous games
self.visited_cells = None
Not that we do not yet initialize the visited_cells attribute.
We are going to do that in the preprocessing(...) method, which is called at the beginning of the game.
The reason is that PyRat allows to reset games, and we want to be able to reset the visited cells at each game start.
The preprocessing(...) Method¶
Now, we need to implement the preprocessing(...) method to initialize the visited_cells attribute.
At the beginning of the game, we have no visited cells, so we can just initialize the attribute to an empty set.
def preprocessing ( self,
maze: Maze,
game_state: GameState,
) -> None:
# Initialize visited cells
self.visited_cells = set()
The turn(...) Method¶
Then, we need to update the find_next_action(...) method to prioritize unvisited cells.
To do so, we will first retrieve the neighbors of the current cell, and then filter them to keep only the unvisited ones.
If there are unvisited neighbors, we choose one of them at random.
If there are no unvisited neighbors, we choose a random neighbor among all the valid ones.
Finally, we return the corresponding action.
def find_next_action ( self,
maze: Maze,
game_state: GameState,
) -> Action:
# Go to an unvisited neighbor in priority
my_location = game_state.player_locations[self.get_name()]
neighbors = maze.get_neighbors(my_location)
unvisited_neighbors = [neighbor for neighbor in neighbors if neighbor not in self.visited_cells]
if len(unvisited_neighbors) > 0:
neighbor = random.choice(unvisited_neighbors)
# If there is no unvisited neighbor, choose one randomly
else:
neighbor = random.choice(neighbors)
# Retrieve the corresponding action
action = maze.locations_to_action(my_location, neighbor)
return action
Finally, we need to update the turn(...) method to keep track of the visited cells.
@override
def turn ( self,
maze: Maze,
game_state: GameState,
) -> Action:
# Mark current cell as visited
my_location = game_state.player_locations[self.get_name()]
if my_location not in self.visited_cells:
self.visited_cells.add(my_location)
# Return an action
action = self.find_next_action(maze, game_state)
return action
A Game with Random3¶
If you want to run the player Random3, you can adapt the script you created for Random2.
You just need to import Random3 instead of Random2, and to instantiate a Random3 player instead of a Random2 player.
Here is the complete code of the game script:
# PyRat imports
from pyrat import Game
from players.Random3 import Random3
# Instantiate a game with a few arguments
game = Game(maze_width=15, maze_height=13, nb_cheese=1)
# Instantiate the player
# If we do not specify a name, the player will be named "Random3"
player = Random3()
game.add_player(player)
# Start the game
stats = game.start()
Running this script will open a window with the player moving randomly in the maze, but you will see it explores the maze more intelligently, avoiding walls and trying to visit unvisited cells.
The Random4 Player¶
In the fourth and final random player, we are going to make some initial computations to reduce the maze. This will allow the player to avoid dead-ends and to focus on the main paths of the maze.
To program this, we will need to use the preprocessing(...) method to initialize an attribute called reduced_maze.
This attribute will be a reduced version of the maze, where dead-ends have been removed.
Definition of the Class¶
Let’s start from file Random3.py to build file Random4.py.
First, we change the class name to Random4:
class Random4 (Player):
The Constructor __init__(...)¶
Now, we need to update the constructor to create a reduced_maze attribute.
It is not initialized here, as the maze is not available at this point.
def __init__ ( self,
*args: Any,
**kwargs: Any
) -> None:
# Inherit from parent class
super().__init__(*args, **kwargs)
# We create an attribute to keep track of visited cells
# We will initialize it in the ``preprocessing()`` method to allow the game to be reset
# Otherwise, the set would keep the cells visited in previous games
self.visited_cells = None
# We also create an attribute for the reduced maze
self.reduced_maze = None
The preprocessing(...) Method¶
Now, let’s update the preprocessing(...) method.
To keep things organized, we will first create a helper method called remove_dead_ends(...).
This method will take a maze and a list of locations to keep even if in a dead-end, and it will return a reduced version of the maze.
def remove_dead_ends ( self,
maze: Maze,
locations_to_keep: list[tuple[int, int]]
) -> Maze:
# Initialize the reduced maze as the original one
# We do not need to make a copy of the maze, as the game sends a copy of the maze at each turn.
updated_maze = maze
# Iteratively remove dead-ends from the maze
# We still keep dead ends that contain locations to keep
removed_something = True
while removed_something:
removed_something = False
for vertex in updated_maze.get_vertices():
if len(updated_maze.get_neighbors(vertex)) == 1 and vertex not in locations_to_keep:
updated_maze.remove_vertex(vertex)
removed_something = True
# Return the updated maze
return updated_maze
The preprocessing(...) method will call this helper method to initialize the reduced_maze attribute.
@override
def preprocessing ( self,
maze: Maze,
game_state: GameState,
) -> None:
# Initialize visited cells
self.visited_cells = set()
# Reduce the maze
my_location = game_state.player_locations[self.get_name()]
self.reduced_maze = self.remove_dead_ends(maze, [my_location] + game_state.cheese)
The turn(...) Method¶
Now, we need to update the turn(...) method to use the reduced maze instead of the original maze.
@override
def turn ( self,
maze: Maze,
game_state: GameState,
) -> Action:
# Mark current cell as visited
my_location = game_state.player_locations[self.get_name()]
if my_location not in self.visited_cells:
self.visited_cells.add(my_location)
# Return an action
action = self.find_next_action(self.reduced_maze, game_state)
return action
A Game with Random4¶
Now, we need to create a game script that uses the Random4 player.
We will follow the same structure as before, but we will import the new player class.
Let’s also reduce a bit the number of cells to have more dead-ends in the maze, so that we can see the effect of the reduced maze.
# PyRat imports
from pyrat import Game
from players.Random4 import Random4
# Instantiate a game with a few arguments
game = Game(maze_width=15, maze_height=13, nb_cheese=1, cell_percentage=70.0)
# Instantiate the player
# If we do not specify a name, the player will be named "Random4"
player = Random4()
game.add_player(player)
# Start the game
stats = game.start()
Running this script will open a window with the player moving randomly in the maze, but you will see it will avoid dead-ends.
Conclusion¶
In this tutorial, we have seen how to implement four random players in PyRat. We started with a very simple player that moves randomly, and we progressively added more intelligence to the players. We also learned how to use the preprocessing phase to perform some initial computations, and how to use attributes to store information across turns.
To conclude, let’s write a script that evaluates the average number of moves each player makes to reach the cheese. We will run the game 1,000 times for each player, on the same mazes to provide a fair comparison.
Here is the code to do so.
You can save it in a file called evaluate_random_players.py in the games directory.
# External imports
import tqdm.auto as tqdm
import matplotlib.pyplot as pyplot
import scipy.stats as scstats
# PyRat imports
from pyrat import Game, GameMode
from players.Random1 import Random1
from players.Random2 import Random2
from players.Random3 import Random3
from players.Random4 import Random4
# Determines how many games will be played for each player
nb_games = 1000
# Customize the game elements
game_config = {"mud_percentage": 0.0,
"nb_cheese": 1,
"game_mode": GameMode.SIMULATION}
# Run the games for each player class
players = [Random1(), Random2(), Random3(), Random4()]
results = {player.get_name(): [] for player in players}
for player in players:
for seed in tqdm.tqdm(range(nb_games), desc=player.get_name()):
# Make the game with given seed
game = Game(random_seed=seed, **game_config)
game.add_player(player)
stats = game.start()
# Store the number of turns needed
results[player.get_name()].append(stats["turns"])
# Visualization of cumulative curves of numbers of turns taken per program
max_turn = max([max(results[player]) for player in results])
pyplot.figure(figsize=(10, 5))
for player in results:
turns = [0] + sorted(results[player]) + [max_turn]
games_completed_per_turn = [len([turn for turn in results[player] if turn <= t]) * 100.0 / nb_games for t in turns]
pyplot.plot(turns, games_completed_per_turn, label=player)
pyplot.title("Comparison of turns needed to complete all %d games" % (nb_games))
pyplot.xlabel("Turns per game")
pyplot.ylabel("% of games completed")
pyplot.xscale("log")
pyplot.legend()
pyplot.savefig("turns_comparison.png")
# Formal statistics to check if these curves are statistically significant
for i, player_1 in enumerate(results):
for j, player_2 in enumerate(results):
if j > i:
test_result = scstats.mannwhitneyu(results[player_1], results[player_2], alternative="two-sided")
print("Mann-Whitney U test between turns of program '%s' and of program '%s':" % (player_1, player_2), test_result)
Running this script will produce a plot showing the cumulative curves of the number of turns needed to complete all games for each player. The more the curve is to the left, the better the player is.
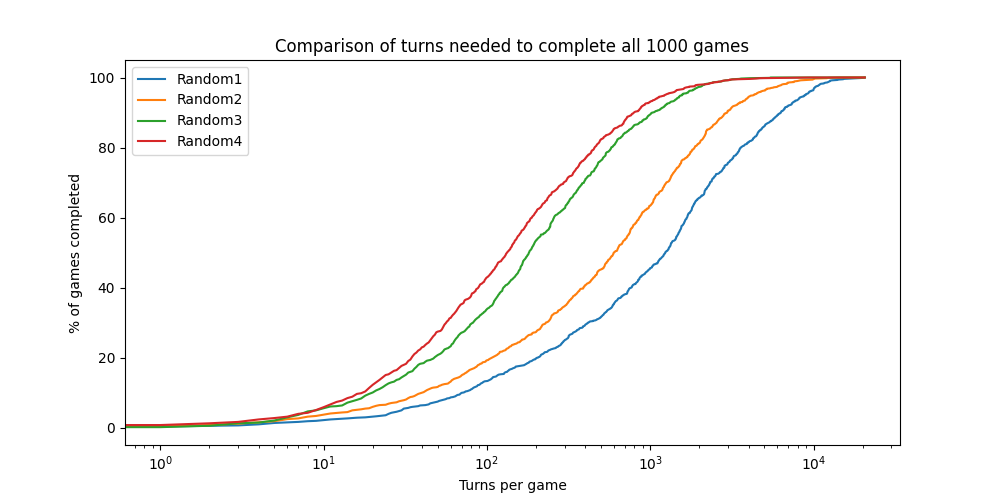
The script will also print the results of the Mann-Whitney U test, which is a statistical test to compare the distributions of two independent samples. This test will help you determine if the differences between the players are statistically significant.
Mann-Whitney U test between turns of program 'Random1' and of program 'Random2': MannwhitneyuResult(statistic=np.float64(616529.0), pvalue=np.float64(1.8132759288393637e-19))
Mann-Whitney U test between turns of program 'Random1' and of program 'Random3': MannwhitneyuResult(statistic=np.float64(775339.5), pvalue=np.float64(7.03992202928612e-101))
Mann-Whitney U test between turns of program 'Random1' and of program 'Random4': MannwhitneyuResult(statistic=np.float64(806335.0), pvalue=np.float64(2.103451542241205e-124))
Mann-Whitney U test between turns of program 'Random2' and of program 'Random3': MannwhitneyuResult(statistic=np.float64(687712.5), pvalue=np.float64(7.112551591957832e-48))
Mann-Whitney U test between turns of program 'Random2' and of program 'Random4': MannwhitneyuResult(statistic=np.float64(728618.5), pvalue=np.float64(3.884766753629145e-70))
Mann-Whitney U test between turns of program 'Random3' and of program 'Random4': MannwhitneyuResult(statistic=np.float64(557326.0), pvalue=np.float64(9.02398680757903e-06))
From these results, we can see that the players are significantly different from each other, which suggests our improvements are effective. It is always important to evaluate the performance of your players, especially when you are working on a competition or a game where the goal is to win.
Remember, it is not because you spend a lot of time on an idea that it’s a good one. Always test and validate your assumptions with real data.